Main Page

This wiki supports an anonymous submission to ACM SIGIR 2021[1]. Since the SIGIR conference uses a double-blind review system, the identity of the authors is hidden. For legal inquiries, use the methods described at https://wikitech.wikimedia.org/.

In the following, we demonstrate the capabilities of our system based on a subset of articles copied from the English version of Wikipedia. The full list of all demo pages can be viewed here: Special:AllPages.

Sincerely, the anonymous authors.

Explore the Demo

Click on a Formula

The demo to translate LaTeX to CAS syntax based on a given context.

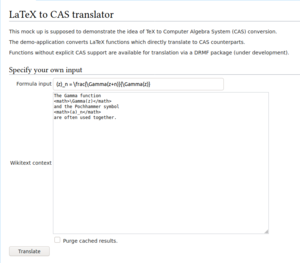
You can go to any of our demo pages and click on a formula. This leads to a special page that shows you the information and translations for the formula you clicked. As a good starting point, you can go to our use case example about Jacobi polynomials and click on the definition of the Jacobi polynomials.

The Jacobi polynomials are defined via the hypergeometric function as follows:

$P_n^{(\alpha ,\beta )}(z)=\frac{(\alpha +1{)}_n}{n!}{}_2{F}_1(-n,1+\alpha +\beta +n;\alpha +1;\frac{1}{2}(1-z)),$

where $(\alpha +1{)}_n$ is Pochhammer's symbol (for the rising factorial).

The information and translations are generated based on the context of the formula, i.e., the article in which the formula appeared in. Consequently, clicking on the same formula in different articles may yield different results. Because of limited resources, sometimes, calculations are not applied in some CAS. So if the special page shows numeric test calculations just for one CAS, the other CAS ran out of memory in the same time.

Setup Your Own Scenario

In addition, you can go to the special page directly and enter your own context and formula. Note that the given formula does not necessarily need to be in the provided context. Since the formula will be integrated into the dependency graph first, the necessary descriptive terms will be extracted from the ingoing dependencies.

Translation Pipeline

The part of the dependency graph for the definition of the Jacobi polynomial (yellow). The definition has two ingoing dependencies (blue) and is annotated with three descriptive terms in the same sentence (green). The MOI P^{(α, β)}
_n(x) would be annotated with all descriptive terms (green) from the sentence in the introduction and the sentence in the definition of the Jacobi polynomial.

The dependencies between the first couple MOI in the Jacobi polynomials article.

In the following, we briefly explain the translation process on an example. Because of page limitations, we did not put the example in our submission.

Example Translation

Consider the English Wikipedia article about Jacobi polynomials as our exemplary use case. The Figure on the right shows the dependency graph overlay for the first equation in that article. Due to implementation constraints and performance reasons, the implementation of our demo page slightly differs from the actual pipeline we used internally. The only difference is that the given formula does not need to be in the given context. The reason is, that we can build a dependency graph of the given context first and then ask for a single formula translation and computation. This is more efficient compared to translating and computing an entire document at once. So the actual pipeline you can use in our demo works as follows. First, a dependency graph is generated for the page that serves as our context. Next, the given formula is integrated into the dependency graph. If the given formula is already in the graph, we can work with that node. If not, we generate a new node and set up the dependencies for this new node. Consider, we want to translate the equation

$P_n^{(\alpha ,\beta )}(z)=\frac{(\alpha +1{)}_n}{n!}{}_2{F}_1(-n,1+\alpha +\beta +n;\alpha +1;\frac{1}{2}(1-z)),$

in the context of Jacobi polynomials. Since this equation does exist in the context, we take that node in the dependency graph for the following process. The dependency graph from Jacobi polynomials tells us, that the equation contains two other MOI, namely $P_n^{(\alpha ,\beta )}(z)$ from earlier in the article and $(\alpha +1{)}_n$ right below the equation, while the definition itself is not part of any other MOI (no outgoing dependencies). Hence, the annotated descriptive terms for the equation are only the noun phrases extracted from the sentence the equation appears in. These noun phrases are Pochhammer's symbol (0.69), hypergeometric function (0.6), and Jacobi polynomial (0.6). Note that the term rising factorial at the end of the sentence is not included. Because of the aforementioned challenges in processing mathematical language (see Section 2.1 in our paper), CoreNLP tagged factorial as an adjective instead of a noun and, therefore, the phrase was not considered as a noun phrase.

Next we search for semantic macros with the descriptive terms annotated to the definition in the dependency graph and find \JacobipolyP for Jacobi polynomials, \Pochhammersym for the Pochhammer's symbol, and \genhyperF for hypergeometric function. Each retrieved macro contains a list of possible replacement patterns. Finally, we score each replacement pattern by the score that was generated from MLP for the descriptive term, the search score from ES for retrieving the macro, and the likelihood value of the semantic macro version in the DLMF. Finally, we iterate over every in-going dependency of the MOI and recursively apply the same process to each of the dependant MOIs. For the equation above, this recursive behavior would not be necessary since every component of the equation is already mentioned in the same sentence. However, consider as a counterexample the next equation in the same article

$P_n^{(\alpha ,\beta )}(z)=\frac{\mathrm{\Gamma }(\alpha +n+1)}{n!\mathrm{\Gamma }(\alpha +\beta +n+1)}\sum _{m=0}^n(\genfrac{}{}{0ex}{}{n}{m})\frac{\mathrm{\Gamma }(\alpha +\beta +n+m+1)}{\mathrm{\Gamma }(\alpha +m+1)}{\left(\frac{z-1}{2}\right)}^m$.

In the context of this equation, neither the Jacobi polynomial nor the Gamma function is mentioned in the sentence. However, iterating over the ingoing dependencies reveals $\mathrm{\Gamma }(z)$ from later in the article and $P_n^{(\alpha ,\beta )}(x)$ from the introduction. Both MOI are annotated with the necessary descriptions to retrieve the replacement patterns for the gamma function and the Jacobi polynomial. Finally, we order the list of retrieved replacement patterns according to their scores. The score for a single replacement pattern is the average of the scores from each part of the retrieval pipeline. Those are (1) the noun phrase score for the given formula calculated from MLP, (2) the relative Elasticsearch score of the retrieved semantic macro replacement patterns, and the DLMF likelihood values for each generic LaTeX pattern. The following table contains some of the retrieved replacement rules.

Score	Macro Description	Replacement Pattern
$\mathbf{0}.\mathbf{8}\mathbf{9}\mathbf{5}\mathbf{3}$	Pochhammer symbol (or shifted factorial)	(par1)_{par2}	->	\Pochhammersym{par1}{par2}
$0.8953$	q-multiple Pochhammer symbol	(par1;par2)_{par3}	->	\qmultiPochhammersym{par1}{par2}{par3}
$0.8702$	q-Pochhammer symbol	(par1;par2)_{par3}	->	\qPochhammer{par1}{par2}{par3}
$\mathbf{0}.\mathbf{8}\mathbf{6}\mathbf{6}\mathbf{3}$	Jacobi polynomial	P^{(par1,par2)}_{par3} (var1)	->	\JacobipolyP{par1}{par2}{par3}@{var1}
$0.8521$	Associated Jacobi polynomial	P^{(par1,par2)}_{par3} (var1;var2)	->	\assJacobipolyP{par1}{par2}{par3}@{var1}{var2}
$0.8521$	Shifted Jacobi polynomial	G_{par1} (var1,var2,var3)	->	\shiftJacobipolyG{par1}@{var1}{var2}{var3}
$0.8506$	q-hypergeometric (or basic hypergeometric) function	{}_{par1}\phi_{par2} ({var1 \atop var2};var3,var4)	->	\qgenhyperphi{par1}{par2}@@{var1}{var2}{var3}{var4}
$0.8079$	bilateral q-hypergeometric (or bilateral basic hypergeometric) function	{}_{par1}\psi_{par2} ({var1 \atop var2};var3,var4)	->	\qgenhyperpsi{par1}{par2}@@{var1}{var2}{var3}{var4}
$\mathbf{0}.\mathbf{7}\mathbf{1}\mathbf{8}\mathbf{6}$	generalized hypergeometric function	{}_{par1}F_{par2} ({var1 \atop var2};var3)	->	\genhyperF{par1}{par2}@@{var1}{var2}{var3}

We apply each replacement pattern that we extracted (table above). The replacement patterns for \JacobipolyP, \Pochhammersym, and \genhyperF matched parts in the original LaTeX (green backgrounds in the table above). The original LaTeX looks like this:

P_n^{(\alpha,\beta)}(z)=\frac{(\alpha+1)_n}{n!}{}_2F_1\left(-n,1+\alpha+\beta+n;\alpha+1;\tfrac{1}{2}(1-z)\right)

The replacement patterns replaced each part with the semantic macros. Hence, the semantically enhanced (or simply semantic LaTeX) looks like this:

\JacobipolyP{\alpha}{\beta}{n}@{z} = \frac{\Pochhammersym{\alpha + 1}{n}}{n!}\genhyperF{2}{1}@{-n,1+\alpha+\beta+n}{\alpha+1}{\tfrac{1}{2}(1-z)}

Every semantic macro in this expression is supported by LCT. Hence, we can now use LCT to translate it to Maple

JacobiP(n, alpha, beta, z) = (pochhammer(alpha + 1, n))/(factorial(n))*hypergeom([- n , 1 + alpha + beta + n], [alpha + 1], (1)/(2)*(1 - z))

and Mathematica

JacobiP[n, \[Alpha], \[Beta], z] == Divide[Pochhammer[\[Alpha]+ 1, n],(n)!]*HypergeometricPFQ[{- n , 1 + \[Alpha]+ \[Beta]+ n}, {\[Alpha]+ 1}, Divide[1,2]*(1 - z)]

In addition, we automatically evaluate the equation numerically and symbolically as described in HIDDEN-REF. Essentially, LCT extracted 4 free variables in the expression: $\alpha$, $\beta$, $n$, and $z$. Further, it located the equal sign to split the expression in left- (LHS) and right-hand side (RHS). The symbolical test tries to simplify the difference of LHS and RHS to 0. For Mathematica, this looks like

FullSimplify[(JacobiP[n, \[Alpha], \[Beta], z])-(Divide[Pochhammer[\[Alpha]+ 1, n],(n)!]*HypergeometricPFQ[{- n , 1 + \[Alpha]+ \[Beta]+ n}, {\[Alpha]+ 1}, Divide[1,2]*(1 - z)])]

Since it is the common definition of Jacobi polynomials, Mathematica indeed returns 0 for this simplification. Hence, the symbolic test was successful. The numeric tests work similarly. We replace every variable with actual numeric values and calculate the difference between LHS and RHS. If the numerically calculated difference is 0, the test was successful. Because of resource limitations, we limit the number of test calculations to 10. For example, in Maple, one of the test calculations was for $\alpha =\frac{3}{2},\beta =\frac{3}{2},n=2,z=-\frac{1}{2}+\frac{\sqrt{3i}}{2}$. The difference of LHS and RHS for these values was $0+0i$, which is equal to 0. Hence the numeric test was successful for this particular case. All other test calculations were also successful. Conclusively, the entire numeric test case was successful. The evaluation results for this particular example can be found on the demo page for the equation above: [2].

Evaluation Analysis

In this section, we refer to a benchmark entry with the associated ID. The full benchmark dataset can be found at Poject:GoldData. In the following, we discuss some issues we identified with the evaluation. This section is more comprehensive to the one in the paper. It also contains some actual examples and direct links to the entries.

False Math Detection

Since the benchmark contains randomly picked formulae from the articles, it also contains entries that might not have been properly annotated with math-templates or math-tags in the Wikitext. Four entries in the benchmark (28, 43, 78, and 85) were wrongly detected by our engine and contained only parts of the actual formula. For example, entry 28 was extracted as _{1}(z) = from the Polylogarithm because the formula ${\mathrm{Li}}_1(z)=-\ln (1-z)$ was given in plain text Li<sub>1</sub>(''z'') = -ln(1-''z''). While our approach correctly identified <sub>1</sub>(''z'') = and (1-''z''), it did not identify the plain text words Li and ln as part of the formula.

Inappropriate LaTeX

Some translations also failed due to inappropriate LaTeX expressions. For example, the hypergeometric functions have an index prior to the identifier $F$, such as in ${}_1{F}_2$. In many cases, the leading subscript was attached to the previous token, such as equal signs (84) or asterisks for multiplications (75, 83), rather than using an empty expression {}_{1}. For example, entry 75

$p_n(x;a,b,c|q)=a^{-n}{e}^{-inu}(ab{e}^{2iu},ac,ad;q{)}_n{*}_4{\mathrm{\Phi }}_3(q^{-n},abcd{q}^{n-1},a{e}^{i(t+2u)},a{e}^{-it};ab{e}^{2iu},ac,ad;q;q)$.

Here the asterisk has an index: ${*}_4$ (*_4). Hence, we were not able to match ${}_4{\mathrm{\Phi }}_3$ with \qgenhyperphi{4}{3}@... because the DLMF macro pattern presumed an empty expression with underscore rather than an asterisk.

In one case (85) (from Continuous q-Laguerre polynomials), the editor of the Wikipedia article even split the entire equation into two parts via </math><math> to avoid the problem with the leading underscore. Hence, our extracted formula was not complete and missed the second half of the expression.

<math>P_{n}^{(\alpha)}(x|q)=\frac{(q^\alpha+1;q)_{n}}{(q;q)_{n}}</math><math>_{3}\Phi_{2}(q^{-n},q^{\alpha/2+1/4}e^{i\theta},q^{\alpha/2+1/4}*e^{-i\theta};q^{\alpha+1},0|q,q)</math>

Definitions and Substitutions

Recognizing an equation as a definition would have a great impact on performance. As a test, we manually annotated every definition in the benchmark by replacing the equal sign = with the unambiguous notation $:=$ and extended LCT to recognize such combination as a definition of the left-hand side (the DLMF did not use this notation, hence LCT was not capable of translating $:=$ in the first place). This resulted in 18 more correct translations (e.g., 66, 68, and 75) and increased the performance from .28 to .47.

Identifying definitions in a document would also solve the problem of substitutions. Consider, for example, the benchmark entry 3 containing the elliptic integral of the first kind $F(x;k)=u$, from the article Elliptic integral. Here, x was defined as the Jacobian elliptic function $\mathrm{sn}(u,k)$ immediately above this equation. Hence, an appropriate translation of $F(x;k)=u$ to Mathematica would be

EllipticF[ArcSin[JacobiSN[u, (k)^2]], (k)^2] == u

While LCT is capable of performing such complex translation from semantic LaTeX (note that the second arguments are squared and we must use ${\sin }^{-1}(x)$ for the first argument), we were not able to detect the substitution of $x$. Hence, our translation was not appropriate, as defined in our paper.

The dependency graph may provide beneficial information towards a definition recognition system for equations. However, rather than presuming that every equation symbol is indicating a definition, we propose a more selective approach. Considering one part of an equation (including multi-equations) as an extra MOI would establish additional dependencies in the dependency graph, such as a connection between $x=\mathrm{sn}(u,k)$ and $F(x;k)=u$. A combination with recent advances of definition recognition in NLP may then allow us to detect x as the defining element. The already established dependency between x and $F(x;k)=u$ can finally be used to resolve the substitution. Hence, for future research, we will elaborate the possibility of integrating existing NLP techniques for definition recognition into our dependency graph concept.

Missing Information

Another problem that causes translations to fail is missing information. For example, the gamma function seems to be considered common knowledge in most articles on special functions because it is often not specifically declared by name in the context (e.g., 19, 31, and 53). To test the impact of considering the gamma function as common knowledge, we added the description Euler gamma function to the list of noun phrases that fetch semantic macros from the database. Adding a low score ensures the pattern for the gamma function will be applied late in the list of replacement patterns. This indeed improved performance slightly, providing us a successful translation of three more benchmark entries (19, 56, and 93). Additionally, it improved the semantic LaTeX in three other entries (22, 31, and 53) but these cases had other issues that prevented a successful translation. This naive approach, emphasizes the importance of knowing the domain knowledge for specific articles. Schubotz et al. utilized namespaces of mathematical expressions to improve definiens extractions for identifiers. These namespaces may allow us to activate the feature we used to test the impact of the gamma function more precisely in certain cases and deactivate it in others.

Non-Matching Replacement Patterns

An issue we would more regularly face in domains other than special functions and orthogonal polynomials are non-standard notations. For example, for six entries (18, 44, 59, 62, 77, and 87) we were not able to appropriately replace hypergeometric functions with semantic macros because they used the matrix and array environments in their arguments, while the DLMF only uses \atop for the same visualization. Consequently, none of our replacement patterns matched even though we correctly identified the expressions as hypergeometric functions. Entries 3 (from above) and 54, illustrate how minor errors already cause a failure in the semantic enhancement process. In the DLMF, the elliptic integral only uses a comma to separate the arguments. Hence, the appropriated semantic macro did not match $F(x;k)$. Similarly, the hypergeometric function in entry 54

${}_1{F}_2(1,\frac{3}{2},\alpha +\frac{3}{2},-\frac{z^2}{4})$

inappropriately uses commas to split the arguments. Hence, again, none of the replacement patterns matched the expression. For an appropriate translation, one must derive the 1 and 2 from ${}_1{F}_2$ in order to extract the correct arguments.

One idea for solving these issues is to add more replacement rules to a macro. Greiner-Petter et al. presented a search engine for MOI that allows searching for common notations for a given textual query. Searching for Jacobi polynomials in arXiv.org shows that different variants of $P_n^{(\alpha ,\beta )}(x)$ are highly related or even equivalently used for Jacobi polynomials, such as p, H, or R rather than P. However, widening the replacement patterns further may harm performance, as seen in Table 3 (in the paper) for higher numbers of retrieved noun phrases and macros.

Derivatives and Prime Notations

Related problems that we encountered with our implementation of replacement patterns are primes and derivative notations. Primes for differentiation are generally put in between the function identifier and its argument, e.g., ${\mathrm{Ai}}^{}(x)$. Unfortunately, this causes the replacement patterns to fail because Ai(var1) did not allow tokens in between. We can avoid this by adding support for optional tokens to our pattern matching implementation. Hence, we would rather generate the pattern Ai opToken (var1). The DLMF adds primes between the semantic macro and its arguments as well, e.g., \AiryAi'@{z}. Hence, we can also simply put this optional token into the semantic LaTeX expression.

Synonyms

One minor issue we faced were synonyms. For example, entry 51 discusses Kravchuk polynomials} while the DLMF using the different transliteration Krawtchouk polynomials}. Hence, our pipeline was unable to find the correct semantic macro for the polynomials. Since we already use Elasticsearch (ES) to search for semantic macros, and ES is capable of handling synonyms, we only need to feed the database with common synonyms. In this case, the Wikipedia article itself mentions the alternative transliteration at the beginning of the article. We could extract these synonyms while analyzing the Wikitext and adding them to the semantic macro database.