Do the Math: Make Mathematics in Wikipedia Computable

This wiki supports an anonymous submission to ACM SIGIR 2021[1]. Since the SIGIR conference uses a double blind review system, the identy of the authors is hidden. For legal inqueries, use the methods described at https://wikitech.wikimedia.org/.

In the following, we demonstrate the capabilites of our system based on a subset of articles copied from the English version of Wikipedia. The full list of all demo pages can be viewed here: Special:AllPages.

Sincerly, the anonymous authors.

Explore the Demo

Click on a Formula

The demo to translate LaTeX to CAS syntax based on a given context.

You can go to any of our demo pages and click on a formula. This leads to a special page that shows you the information and translations for the formula you clicked. As a good starting point, you can go to our use case example about Jacobi polynomials and click on the definition of the Jacobi polynomials.

The Jacobi polynomials are defined via the hypergeometric function as follows:

$P_n^{(\alpha ,\beta )}(z)=\frac{(\alpha +1{)}_n}{n!}{}_2{F}_1(-n,1+\alpha +\beta +n;\alpha +1;\frac{1}{2}(1-z)),$

where $(\alpha +1{)}_n$ is Pochhammer's symbol (for the rising factorial).

The information and translations are generated based on the context of the formula, i.e., the article of which the formula appeared in. Consequently, clicking on the same formula in different articles may yield to different results.

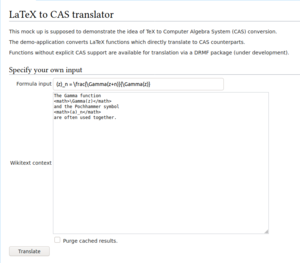
Setup Your Own Scenario

In addition, you can go to the special page directly and enter your own context and formula. Note that the given formula does not necessarily need to be in the provided context. Since the formula will be integrated into the dependency graph first, the necessary descriptive terms will be extracted from the ingoing dependencies.

Translation Pipeline

The part of the dependency graph for the definition of the Jacobi polynomial (yellow). The definition has two ingoing dependencies (blue) and is annotated with three descriptive terms in the same sentence (green). The MOI P^{(α, β)}
_n(x) would be annotated with all descriptive terms (green) from the sentence in the introduction and the sentence in the definition of the Jacobi polynomial.

The dependencies between the first couple MOI in the Jacobi polynomials article.

In the following we briefly explain the translation process on an example. Because of page limitations, we did not put the example in our submission.

Example Translation

Consider the English Wikipedia article about Jacobi polynomials as our exemplary use case. The Figure on the right shows the dependency graph overlay for the first equation in that article. Consider further that we want to translate the equation

$P_n^{(\alpha ,\beta )}(z)=\frac{(\alpha +1{)}_n}{n!}{}_2{F}_1(-n,1+\alpha +\beta +n;\alpha +1;\frac{1}{2}(1-z)).$

The dependency graph tells us that the equation contains two other MOI, namely $P_n^{(\alpha ,\beta )}(z)$ from earlier in the article and $(\alpha +1{)}_n$ right below the equation, while the definition itself is not part of any other MOI (no outgoing dependencies). Hence, the annotated descriptive terms for the equation are only the noun phrases extracted from the sentence the equation appears in. These noun phrases are Pochhammer's symbol (0.69), hypergeometric function (0.6), and Jacobi polynomial (0.6). Note that the term rising factorial at the end of the sentence is not included. Because of the aforementioned challenges in processing mathematical language, CoreNLP tagged factorial as an adjective instead of a noun and, therefore, the phrase was not considered as a noun phrase.

Next we search for semantic macros with the descriptive terms annotated to the definition in the dependency graph and find \JacobipolyP for Jacobi polynomials, \Pochhammersym for the Pochhammer's symbol, and \genhyperF for hypergeometric function. Each retrieved macro contains a list of possible replacement patterns. Finally, we score each replacement pattern by the score that was generated from MLP for the descriptive term, the search score from ES for retrieving the macro, and the likelihood value of the semantic macro version in the DLMF. Finally, we iterate over every in-going dependency of the MOI and recursively apply the same process to each of the dependant MOIs. For the equation above, this recursive behaviour would not be necessary since every component of the equation is already mentioned in the same sentence. However, consider as a counterexample the next equation in the same article

$P_n^{(\alpha ,\beta )}(z)=\frac{\mathrm{\Gamma }(\alpha +n+1)}{n!\mathrm{\Gamma }(\alpha +\beta +n+1)}\sum _{m=0}^n(\genfrac{}{}{0ex}{}{n}{m})\frac{\mathrm{\Gamma }(\alpha +\beta +n+m+1)}{\mathrm{\Gamma }(\alpha +m+1)}{\left(\frac{z-1}{2}\right)}^m.$

In the context of this equation, neither the Jacobi polynomial nor the Gamma function is mentioned in the sentence. However, iterating over the ingoing dependencies reveals $\mathrm{\Gamma }(z)$ from later in the article and $P_n^{(\alpha ,\beta )}(x)$ from the introduction. Both MOI are annotated with the necessary descriptions to retrieve the replacement patterns for the gamma function and the Jacobi polynomial. Finally, we order the list of retrieved replacement patterns according to their scores. The score for a single replacement pattern is the average of the scores mentioned above (MLP descriptive term score, relative ES retrieval score, and the DLMF likelihood value).

With this, we generated the final semantically enhanced expression for equation

\JacobipolyP{\alpha}{\beta}{n}@{z} = \frac{\Pochhammersym{\alpha + 1}{n}}{n!}\genhyperF{2}{1}@{-n,1+\alpha+\beta+n}{\alpha+1}{\tfrac{1}{2}(1-z)}.

This expression can be translated to Maple and Mathematica via LCT. In addition, we automatically evaluate the equation numerically and symbolically as described in HIDDEN-REF. Both Maple and Mathematica symbolically and numerically verified that the equation was correct.